portable-antennas

Coaxial Cable
Coax type:	Sort list by: Type Diameter Max. frequency	Remarks
Impedance:		Outer diameter:	Max. frequency:
Weight per 10m:		Velocity factor:	Capacitance/m:
Manufacturer:		Sheath type:
Inner Conductor
Type:		Diameter:
Dielectric
Type:		Diameter:
Cable Screen
Type:		Diameter:
Data Reference:

Reference charts and diagrams

A collection of charts and diagrams displaying various correction factors used in the designer pages

Chart of end-effect correction factors

An end-effect correction factor is applied to calculations of antenna wire lengths, and is dependent on the ratio of wavelength to wire diameter, the λ/d ratio.

This λ/d ratio can take a wide range of values, as shown by this table:

λ/d ratios by band and wire diameter

Calculate your own end-effect correction factor:
Frequency:	MHz Wavelength λ: meters
Wire diameter d:	mm
λ/d ratio:
Correction factor:

Chart of dipole feed-point impedance vs. apex angle

A flat dipole in free space has a characteristic feed-point impedance of ~73.1 Ω. When situated above real ground, however, the impedance will be somewhat less.

When a dipole is configured as an inverted vee, the feed-point impedance will depend on the included apex angle of the antenna: the smaller the apex angle, the smaller the impedance.

Feed-point impedance by apex angle

The table and chart show the variation by included apex angle for an inverted-vee dipole in ideal conditions over perfectly conducting ground.

It is recommended to keep the included apex angle between 90° and 180° - if it is less than 90°, the feed-point impedance rapidly decreases, thereby lowering the radiation resistance, and will lead to increased coupling between the two legs of the antenna. This will result in poor antenna performance.

Chart of dipole feed-point impedance vs. antenna height

A flat dipole in free space has a characteristic feed-point impedance of ~73.1 Ω. When situated above real ground, however, the impedance will be somewhat less.

When a dipole is situated above real ground, its' feed-point impedance is found to vary with its' height above the ground.

Feed-point impedance by antenna height

The table and chart show the variation by height in wavelengths above ground for a flat dipole in ideal conditions over a perfectly conducting ground.

Situating a dipole antenna too low above the ground can result in a low feed-point impedance, low radiation resistance, and increased capacitive coupling of the RF field with the ground, leading to poor antenna performance.

Chart of inverted-Vee dipole length correction factor vs. antenna apex angle

A flat dipole in free space will resonate at its' design frequency. In the real world, however, in a dipole configured as an inverted-vee, the resonant frequency will be found to increase with the antenna's central apex angle, while the bandwidth at resonance will decrease.

In order to counteract such an increase in resonant frequency, it is necessary to lengthen the dipole "legs" by a small amount, dependent on the apex angle, to bring the antenna to resonance at the desired frequency.

Inverted-vee dipole - length correction
factors by apex angle

The table and chart show the variation by apex angle for a dipole configured as an inverted vee.

An inverted-vee dipole antenna with an apex angle between 180° (a flat-top) and 90° will function well; angles below 90° will result in poor performance.

Reference wire insulation factors

Charts and diagrams displaying wire-insulation length-correction factors used in the designer pages

Charts of wire-insulation length-correction factors

Radio engineers and radio amateurs have long known that, when a wire antenna is made from insulated wire, the insulation will increase the electrical length of the wire to a degree which depends on the wire diameter, the insulation thickness, and the insulation material.

For insulated wires, therefore, it is necessary to include a suitable length-correction factor to compensate for the electrical lengthening due to the insulation. These charts list such factors by:

insulator type, wire diameter and insulation thickness;
wire diameter, insulator type and insulation thickness.

The values presented here are empirically derived from results obtained from multiple runs of the NEC v4.2 engine, for combinations of various insulator material types, wire core diameters, and insulator thicknesses.

1. Wire insulation correction factors by insulator type:

2. Wire insulation correction factors by wire diameter: mm

Interested parties may download the insulation correction-factors data as a CSV file.

Frequency / wavelength calculator

Speed of light:	m/s in vacuum in air
Frequency:
Wavelength:

Convert VSWR value to power loss

Any value of VSWR higher than 1:1 can cause power loss due to reflected RF being dissipated in the feeder line: use this to calculate how much power loss is due to VSWR

Power input:	W
VSWR value:	: 1
Mismatch loss:	dB
Percentage loss;	%
Reflection coefficient:
Percentage output:	%
Power output:	W

Metric to Imperial units calculator

Convert meters to decimal feet, or
Convert decimal feet to meters

Meters:	m
Feet:	ft =

Convert reactance value to inductance or capacitance value

Frequency:	MHz
Reactance:	Ω
Inductance:	µH
Capacitance:	pF

Decibel calculator

Add or subtract two decibel (dB) values

Decibel value #1:	dB
Decibel value #2:	dB
Result:	dB

Quarter-wave line matching transformer

The 1/4-wave line matching transformer, also known as a Q-section, is a section of feed-line having a specific impedance designed to transform an input impedance to a different output impedance.

This can be useful when connecting feedlines of different impedances: say, a length of 50Ω coaxial line to a length of 75Ω coaxial line.

The matching 1/4-wave section is connected in series between the input line and the output line, or load.

First impedance, Z_in	Ω
Second impedance, Z_L	Ω
Matching impedance, Z₀	Ω

Calculation of losses due to transmission line

Real HF transmission lines, such as coaxial cable or ladder line, are not perfect conductors of HF energy, and will therefore lead to a certain amount of RF signal loss. Depending on the type and length of transmission line, and the operating frequency, these losses can be quite substantial.

For single-band antennas, such losses are negligible around the resonant frequency. For multi-band antennas - such as OCFD, EFHW antennas, and half-square antennas configured as voltage-fed EFHWs - the losses are also negligible at the various resonant frequencies, but become very significant at frequencies where the antenna is not resonant:

40-meter EFHW antenna - chart of VSWR at the feed-point

In this example, showing only VSWR values at the antenna feed-point, very high VSWR values are seen at the frequencies where the antenna is not resonant, i.e at the 30m, 17m and 12m bands.

By introducing a configurable length and type of coax cable into the analysis, however, it is possible to transform such high values to ones more accessible to the average antenna tuner:

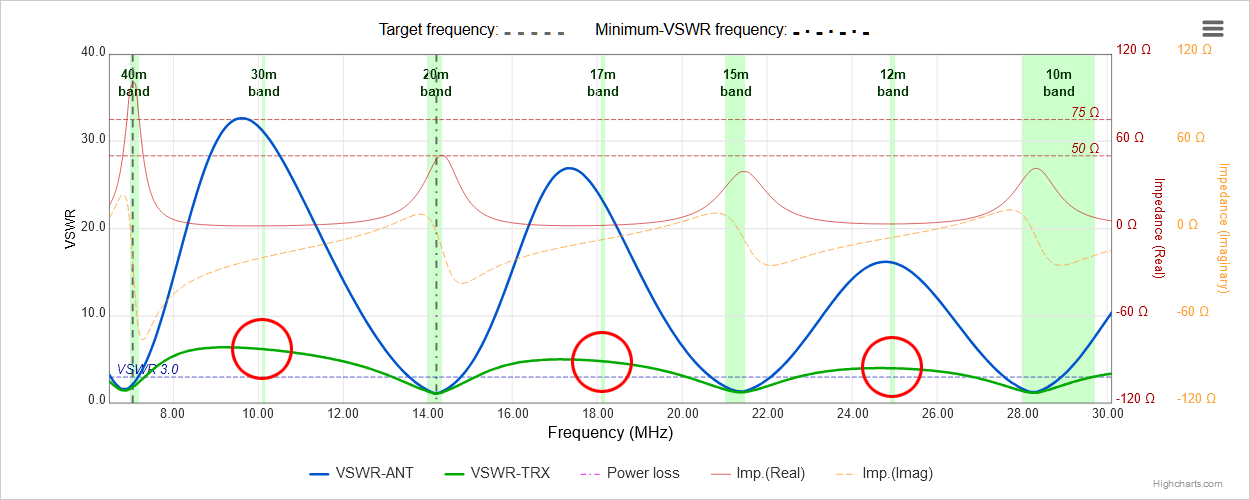
40-meter EFHW antenna - chart of VSWR at feed-point, and at the transmitter end of a length of coax

Here, the green curve shows the VSWR values to be expected at the transmitter end of a length of coax (in this example, 12 meters of RG-316 U coax). It is apparent that the resulting VSWR values at the 30m, 17m and 12m bands are much more amenable to tuning below 3:1 by an antenna tuner; it should be understood that this comes at the penalty of higher signal loss.

The following section shows how such losses, and hence VSWR curves at the transmitter end of a length of coax, are calculated.

The input impedance of a real, lossy transmission line is computed using the Transmission Line Equation which can take several forms. Here we use a variation using hyperbolic trigonometric functions, after ARRL Antenna Book, 20th Edition, p. 24-12:

$Z_{in} = Z_{0} \frac{Z_{L} cosh (γ l) + Z_{0} sinh (γ l)}{Z_{L} sinh (γ l) + Z_{0} cosh (γ l)}$

We expand this expression in order to separate out the real and imaginary parts in the sinh and cosh arguments.

$Z_{in} = Z_{0} \frac{Z_{L} cosh (l (α + j β)) + Z_{0} sinh (l (α + j β))}{Z_{L} sinh (l (α + j β)) + Z_{0} cosh (l (α + j β))}$

This second expression is then expanded fully, using standard identities for hyperbolic sines and cosines of complex numbers. This is the basis of the code used to calculate the value of Z_in .

$Z_{in} = Z_{0} \frac{Z_{L} (cosh (l α) * cos (l β) + j sinh (l α) * sin (l β)) + Z_{0} (sinh (l α) * cos (l β) + j cosh (l α) * sin (l β))}{Z_{L} (sinh (l α) * cos (l β) + j cosh (l α) * sin (l β)) + Z_{0} (cosh (l α) * cos (l β) + j sinh (l α) * sin (l β))}$ Eq. (1)

where
$Z_{in} =$ complex impedance at input of coax line
$Z_{L} =$ complex load impedance at end of coax line, i.e. at the antenna $= R_{a} \pm j X_{a}$
$Z_{0} =$ characteristic impedance of coax line $= R_{0} + j X_{0}$
$l =$ physical length of coax line in meters
$γ =$ complex loss coefficient $= α + j β$
$α =$ matched line loss attenuation constant, in nepers per unit length
(1 neper = 8.68589 dB; cables are rated in dB per 100 meters)
$β =$ phase constant of coax line in radians per unit length
$= \frac{2 π}{F_{v} L_{w}}$ for $F_{v} =$ velocity factor of coax line, and $L_{w} =$ wavelength $= \frac{300}{f_{MHz}}$

Since, for a given setup, all of these values except frequency are constant, $Z_{in}$ will vary with frequency.

Once the value of $Z_{in}$ has been established for a particular combination of antenna, coax feed-line and frequency, we use the following expression (from a letter in the Technical Correspondence section of QST magazine, November 1997, p70-71) to calculate the loss in dB due to VSWR:

$L_{VSWR} = 10 {log}_{10} (\frac{(1 - | ρ_{in} |^{2})}{(1 - | ρ_{L} |^{2})})$ Eq. (2)

where
$L_{VSWR} =$ loss in dB due to VSWR
$| ρ_{in} | = the magnitude of (Z_{in} - Z_{0}^{*}) / (Z_{in} + Z_{0})$
$| ρ_{L} | = the magnitude of (Z_{L} - Z_{0}^{*}) / (Z_{L} + Z_{0})$
$Z_{0}^{*} = complex conjugate of the feed-line characteristic impedance R_{0} + j X_{0}$

This expression avoids problems associated with possibly negative values of VSWR by using complex impedances and thus eliminating VSWR from the calculation.

In calculating losses for a particular combination of antenna and coax feed-line over several frequencies, it is necessary to calculate both equations 1 and 2 for each frequency. The number of frequencies covered for a VSWR curve over a single band is on the order of 40 or 50.

Extras - Useful Tools

Coax cables - charts and data

Convert dB attenuation to power loss

Chart of losses in dB against coax length, for multiple coax types, at a single frequency